New Paper on "on the Importance of self-consistency in Recurrent Neural Network Models Representing Elasto-plastic Solids

Abstract

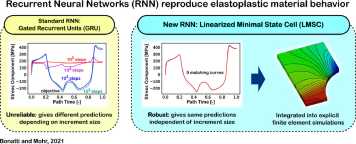
Recurrent neural networks could serve as surrogate material models, removing the gap between component-level finite element simulations and numerically costly microscale models. Recent efforts relied on gated recurrent neural networks. We show the limits of that approach: these networks are not self-consistent, i.e. their response depends on the increment size. We propose a recurrent neural network architecture that integrates self-consistency in its definition: the Linearized Minimal State Cell (LMSC). While LMSCs can be trained on short sequences, they perform best when applied to long sequences of small increments. We consider an elastoplastic example and train small models with fewer than 5’000 parameters that precisely replicate the deviatoric elastoplastic behavior, with an optimal number of state-variables. We integrate these models into an explicit finite element framework and demonstrate their performance on component-level simulations with tens of thousands of elements and millions of increments.